CAMBIO DE VARIABLE

 

CAMBIO DE VARIABLE




El método del cambio de variable es una técnica comúnmente utilizada en cálculo para simplificar integrales definidas o resolver ecuaciones diferenciales. La idea principal es sustituir una variable por otra que simplifique el problema o lo haga más manejable.

Aquí tienes los pasos generales para realizar un cambio de variable en una integral definida:

Elige una nueva variable: Decide qué variable deseas introducir en lugar de la original. Esta nueva variable debe ser una función suave y biyectiva de la original, lo que significa que la función debe ser continua y tener una inversa definida.


Encuentra la relación entre las variables: Expresa la nueva variable en términos de la original, es decir, encuentra la función de cambio. Por ejemplo, si decides cambiar de x a u, necesitas encontrar una función u=g(x).


Calcula la derivada de la función de cambio: Si la función de cambio no es lineal, necesitarás calcular su derivada du/dx. Esto te ayudará a ajustar los límites de integración correctamente.


Sustituye en la integral: Reemplaza la variable original y su diferencial en la integral con la nueva variable y su diferencial, utilizando la función de cambio y su derivada si es necesario.


Ajusta los límites de integración: Si has cambiado la variable de integración, también necesitarás ajustar los límites de integración. Esto se hace utilizando la función de cambio.


Resuelve la integral con la nueva variable y los nuevos límites: Ahora, resuelve la integral resultante utilizando la nueva variable y los límites ajustados.


Expresa la solución en términos de la variable original: Si es necesario, expresa la solución final en términos de la variable original.


Verifica la solución: Siempre es importante verificar que la solución obtenida sea válida y cumpla con las condiciones del problema original.










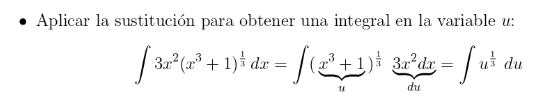
Comentarios

Publicar un comentario

Entradas más populares de este blog

Capas Cilindricas

Imagen
  CALCULO DE VOLUMENES MEDIANTE CAPAS CILÍNDRICAS  EJEMPLO Definamos R como la región delimitada por el gráfico de f(x)=2x–x2 y abajo por el eje x en el intervalo [0,2]. Calcule el volumen del sólido de revolución que se forma al girar R alrededor del eje y. El método de capas cilíndricas es una técnica comúnmente utilizada en cálculo integral para encontrar el volumen de sólidos cuya sección transversal puede describirse mediante funciones. Consiste en dividir el sólido en capas delgadas, cada una modelada como un cilindro o un anillo, y luego sumar el volumen de todas estas capas para obtener el volumen total. Voy a mostrarte cómo se puede aplicar este método para encontrar el volumen de un sólido utilizando un ejemplo concreto: Supongamos que queremos encontrar el volumen del sólido que se forma al girar la región delimitada por la función � = � 2 y = x 2 y el eje � x sobre el intervalo [ 0 , 1 ] [ 0 , 1 ] . Definición de capas cilíndricas : Dividimos el intervalo [ 0 , 1...
Leer más

Derivadas de Orden Superior

Imagen
Las derivadas de orden superior  son derivadas de funciones que ya han sido derivadas una o más veces. La primera derivada de una función se denota comúnmente como f′(x) y representa la tasa de cambio instantánea de la función en un punto dado. La segunda derivada, denotada como f′′(x), es la derivada de la primera derivada y representa la tasa de cambio de la tasa de cambio, es decir, la aceleración. Por ejemplo, si � ( � ) f ( x ) es una función, entonces la segunda derivada � ′ ′ ( � ) f ′′ ( x ) se puede obtener derivando dos veces � ( � ) f ( x ) con respecto a � x . Matemáticamente, se expresa como: � ′ ′ ( � ) = � 2 � � 2 � ( � ) f ′′ ( x ) = d x 2 d 2 ​ f ( x ) Ejemplos: Nota: Para después de la 4ta Derivada se tiene  que encerrar el número de la derivada en paréntesis. si cambiamos  las X por un mero como el 1 nos quedaría  de la siguiente  manera Informacion Adicional: Las derivadas de orden superior son sucesivas derivadas de una función con respec...
Leer más