Integracion de Potencias Trigonometricas
Cuando las integrales presentan potencias de funciones trigonometricas es necesario utilizar diferentes identidades que permitan optener una nueva expresion trigonometrica mas sencilla para facilitar la integracion mas sencilla.
1.- Para funcion Seno.
1.1 Si las potencias san impares deveras emplear:


La integración de potencias trigonométricas puede ser un poco complicada, pero se puede abordar utilizando diversas técnicas, como sustituciones trigonométricas, identidades trigonométricas y partes. Aquí tienes algunos ejemplos:
Integración de potencias de seno y coseno: Para integrar potencias de seno y coseno, puedes usar las identidades trigonométricas para simplificar la expresión. Por ejemplo:
Donde y son enteros no negativos, puedes utilizar identidades como o para reducir la potencia más alta y luego aplicar una sustitución.
Integración de potencias de tangente y secante: Integrar potencias de tangente y secante a menudo implica utilizar identidades trigonométricas o sustituciones trigonométricas para simplificar la expresión. Por ejemplo:
Puedes utilizar identidades como o para simplificar la expresión antes de integrar.
Integración de productos de seno y coseno: Si tienes una expresión que contiene productos de seno y coseno, puedes usar identidades trigonométricas como para simplificar la integral.
Integración de potencias de funciones trigonométricas con potencias pares: Cuando tienes potencias pares de funciones trigonométricas, puedes utilizar identidades como o para reducir la potencia y luego integrar.
Integración de potencias de funciones trigonométricas con potencias impares: Las potencias impares de funciones trigonométricas pueden ser más complicadas de integrar, pero a menudo puedes usar una sustitución trigonométrica para simplificar la expresión.


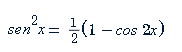

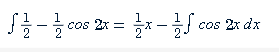


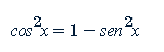








Comentarios
Publicar un comentario